Bugün öğrendim ki: Langton'ın Karıncası hakkında, bir "karıncanın" sadece iki kurala sahip bir ızgara üzerinde hareket ettiği, binlerce kaotik adım ürettikten sonra sonunda sonsuz, tekrarlayan bir otoyol düzeni oluşturduğu basit bir bilgisayar simülasyonu.
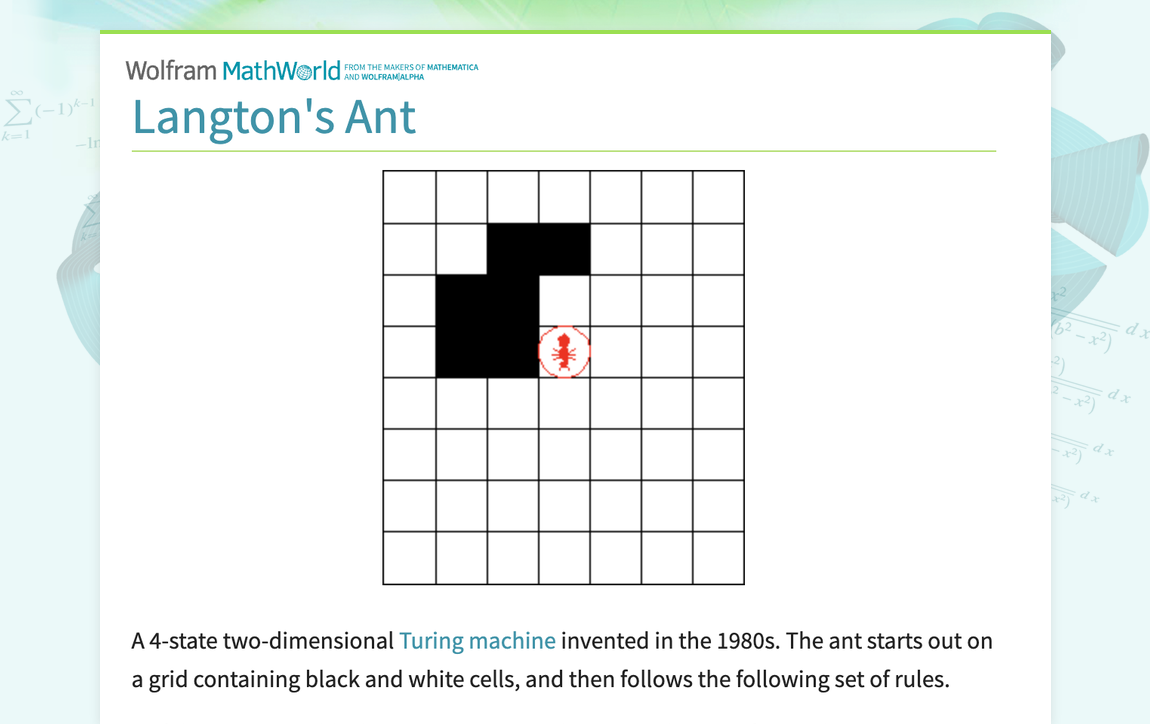
1980'lerde icat edilen 4 durumlu iki boyutlu bir Turing makinesi. Karınca, siyah ve beyaz hücreler içeren bir ızgarada başlar ve aşağıdaki kuralları izler.
1. Karınca siyah bir karedeyse, sağa döner ve bir birim ileri hareket eder.
2. Karınca beyaz bir karedeyse, sola döner ve bir birim ileri hareket eder.
3. Karınca bir kareden ayrıldığında, rengini tersine çevirir.
Karınca boş bir ızgarada başlatıldığında, sonunda sonsuza dek tekrar eden 104 adımlı bir "otoban" oluşturur; her seferinde karıncayı dikey ve yatay olarak iki piksel yer değiştirir. Yukarıdaki grafikler, karıncanın tamamen beyaz bir ızgaradan 386 (sol şekil) ve (sağ şekil) adımdan sonra başlamasını göstermektedir. Sağdaki şekilde, otoban sağ alt köşeye doğru inşa edilmektedir. Karıncanın yolunun sınırsız olması, Cohen-Kung teoremiyle garanti edilir. Karıncanın başlangıçta hangi desende başlatılırsa başlatılsın, sonunda bir otoban oluşturacağına inanılmaktadır (ancak bu noktaya ulaşması çok uzun sürebilir). Bu, Langton's karıncasının tersine çevrilebilir olmasından doğal olarak kaynaklanıyor gibi görünse de, resmi olarak kanıtlanmamıştır (Beermann ve Van Foeken).
2009 yılında Benedetti birçok davranışın videosunu yayınladı.