Bugün öğrendim ki: Augustus'tan (MS 14) Theodosius'a (MS 395) kadar birleşik Roma İmparatorluğu'nun 69 imparatorundan 43'ü şiddet yoluyla öldü, yani %62'si suikast (en yaygın ölüm şekli), intihar veya Roma'nın yabancı bir düşmanıyla çatışma sırasında öldü.

---

Bir Roma imparatorunun bir gladyatörle ortak noktası neydi? İkincisinin bir dövüşten sağ kurtulma şansı, birincisinin şiddetli bir ölümden kaçınma şansından daha yüksekti.

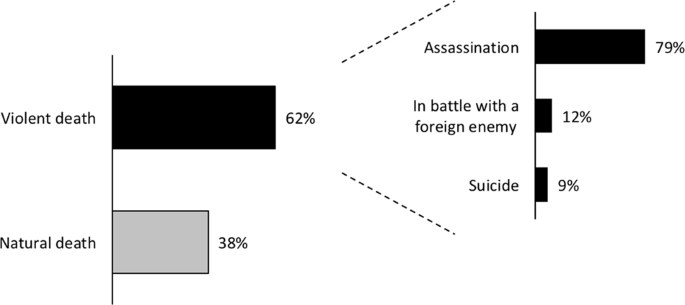
Popüler kültür, Roma imparatorlarının yaşamlarını geleneksel olarak lüks, zulüm ve sefahatle ilişkilendirir, bazen haklı olarak. Bu listede eksik olan özellik, şaşırtıcı bir şekilde, bu güçlü görevin sahibi için en tehlikeli olmasıdır, istatistikler bunu gösterecektir. Şunları göz önünde bulundurun: Avgustus'tan (ö. 14 MS) Theodosius'a (ö. 395 MS) kadar birleşik Roma İmparatorluğu'nun 69 hükümdarından 43'ü, yani %62'si suikast (en yaygın ölüm şekli), intihar veya Roma'nın yabancı bir düşmanıyla savaş sırasında şiddetli ölüm yaşamıştır.1 (Şekil 1). Bu istatistiği bağlama oturtmak ve büyüklüğünü daha iyi anlamak için, günümüzde ciddi derecede tehlikeli bir faaliyet olarak kabul edilen bir şeyle karşılaştırın: Himalaya dağcılığı. Himalayalar'da 8000 m'nin üzerinde zirve yapan dağcıların ölüm riski yaklaşık %4'tür; bu, son 50 yıldır nispeten tutarlı bir rakamdır (Amalberti vd., 2005). Roma imparatorlarının şiddetli ölüm riski, bu cesur dağcılardan bir kat daha fazlaydı.

Bir Roma imparatorunun hayatta kalma olasılığı, altı gözlü bir tabancayla Rus ruleti oynamaya kabaca eşdeğerdi; katılımcı bir değil dört mermi yerleştiriyor, sonucu rastgele hale getirmek için silindiri çeviriyor ve namluyu başına dayayarak tetiği çekiyordu.

Bu uğursuz karşılaştırma, hikayemizin merkezinde yer alan ana kahraman olan rastgele değişken kavramını çağrıştırıyor. Bir imparator için şiddetli ölüm olasılığının yüksek olduğu, nicel olarak değilse de nitel olarak, Edward Gibbon'ın Roma İmparatorluğu'nun Yükselişi ve Düşüşü'nün ilk cildinin yayınlanmasından (1776) beri biliniyordu. Üçüncü yüzyıldaki sorunlu dönemde imparatorluğu yeniden kuran (Watson, 1999) "dünyanın yeniden kurucusu" lakaplı son derece enerjik İmparator Aurelian'dan (270-275 yılları arasında hüküm sürmüştür) bahsederken, Gibbon'ın imparatorun öldürülmesiyle ilgili hayal kırıklığını neredeyse hissedebiliriz.2:

Roma imparatorlarının talihsiz durumu şuydu ki, davranışları ne olursa olsun kaderleri genellikle aynıydı. Zevk veya erdem, sertlik veya yumuşaklık, tembellik veya şan dolu bir yaşam, zamanından önce bir mezara götürdü; ve neredeyse her saltanat, ihanet ve cinayetin aynı iğrenç tekrarıyla sona erdi [vurgu eklendi].

Daha sonra, "Roma senatörleri, başka bir imparatorun kampında öldürüldüğünü şaşkınlık duymadan dinlediler" diye ekledi.

Bu noktada, Gibbon'ın bahsettiği bu ihanet ve cinayet sicilinin başlamasından önceki zamana, popüler bir dönüm noktası alıntısını yeniden ziyaret etmek ve yeni bir ışık altında anlamak için küçük bir tarihsel gezintiye çıkmaya değer, Julius Caesar'ın "Iacta alea est"...

Zar ve insanlar. Ve Roma imparatorları

Sezar, lejyonuyla sığ Rubicon nehrini geçme kararını düşündüğünde - hem kendisi hem de askerleri için büyük bir suç - Suetonius'a göre, "iacta alea est" diye bağırdığı söylenir (Suetonius, 1998). İfade genellikle "zar atıldı" veya daha kararlı bir şekilde "zar atsın" şeklinde çevrilir ve geri dönüşü olmayan bir eylemde geri dönüş noktasının geçmesini ifade eder. Roma askerlerinin ve birkaç imparatorun düşkün olduğu zar oyununa aşina olan herkes için, ünlemin vurgusu geri dönüş noktasının geçmesinden çok olası sonucun rastgele doğasına daha çok odaklanır. Sonucun, örneğin, tek sayı olma olasılığı nedir? Ya da dört yüzlü veya altı yüzlü bir zar verildiğinde belirli bir sayı? Sezar hangi sonuçları düşündü? Açıkçası, girişiminin kaderi var: Roma Cumhuriyeti devam edecek mi, yoksa bu tabutuna son çivi mi? Kendi kaderi ne olacak? Başarılı olacak mı, yoksa şiddetli bir ölümle mi karşılaşacak? Rubicon'u geçerek Sezar, karşılaşabileceği olası sonuçların kapsamını önemli ölçüde daralttı.

Bu orijinal zar atmanın ötesinde, Sezar yalnızca kendisi için değil, her sonraki imparator için de bir metafor sağladı: senato tarafından onaylandıktan veya lejyonlar veya pretoryen muhafızları tarafından seçildikten sonra, her imparator "iacta alea est" diye bağırabilir ve aslında hayatı için zar atıyordu. Geriye dönüp baktığımızda, birleşik Roma İmparatorluğu'nun hükümdarlarının toplu olarak şiddetli bir ölümle ölme şansının %62 olduğunu biliyoruz. Bu, örneğin {1, 2, 3, 4} sonuçlarını bu korkunç sonla ilişkilendirmeye ve altı yüzlü adil bir zar atmaya kabaca eşdeğerdir. Sadece 5 veya 6 atanlar doğal nedenlerden öldü. Bu, önceki Rus ruletinden daha iyi huylu ama aynı derecede güçlü bir metafordur.

Ancak bilinmeyen ve bugüne kadar hiç incelenmeyen şey, bu hükümdarlarla ilişkili başka bir rastgele değişken olan arıza zamanları veya şiddetli ölüm zamanıdır. Bu fikri ve bu çalışmanın odağını daha iyi anlamak için biraz güvenilirlik mühendisliği tartışması yapılmalıdır.

Güvenilirlik, yıllardır bir kişinin veya bir ekipmanın övülebilir bir özelliği olarak kutlanan popüler bir kavramdır. İngilizce dilindeki birçok kelime Shakespeare tarafından uydurulmuş veya ona atfedilmiş olsa da, güvenilirlik kelimesini başka bir İngiliz yazar olan şair Samuel Coleridge'e (1772-1834) borçlu olduğumuz anlaşılıyor. Coleridge, bir arkadaşını överken şunları yazdı (Coleridge, 1983; Saleh ve Marais, 2006):

Düzensiz insanlar etraflarına saçtıkları ve toplamda hem mutluluğa hem de faydaya sık sık büyük engeller haline gelen bu küçük acıları ve rahatsızlıkları hiç yaşatmaz; aksine, etrafındakilere veya kendisiyle bağlantılı olanlara tüm zevkleri bahşeder ve onlara mükemmel bir tutarlılıkla ve (böyle bir kelime oluşturulabilirse) mutlak güvenilirlikle zihnin rahatlığını ilham eder.

O zamandan beri, güvenilirlik mühendisliği, modern, teknolojik olarak yoğun dünyamızın birçok yönüne yayılan önemli bir disiplin haline geldi (Hoyland ve Rausand, 2009). Güvenilirlik mühendisliğindeki temel fikir, bir eşyanın arıza zamanının, Tf, stokastik doğada olması, bir rastgele değişken olmasıdır. Kabaca konuşursak, güvenilirlik, S(t), bir eşyanın t zamanında hala çalışır durumda olma olasılığı olarak tanımlanır; başarısız olmamıştır ve bu zamana kadar işlevini yerine getirmektedir:

$$S\left( t \right) \equiv {\mathrm{Pr}}\left( {T_{\mathrm {f}}\; > \;t} \right)$$

(1)

S(t) aynı zamanda hayatta kalma veya hayatta kalan fonksiyonu olarak da bilinir. Güvenilirlik mühendisliği daha sonra bu olasılığı bir eşyanın ömrü boyunca nicelleştirmekle ilgilenir. Bu, amaçlarımız için yeterlidir. Güvenilirlik mühendisliğinde faydalı bir başka kavram da arıza oranıdır. Hikayemiz için daha az önemlidir ancak bahsetmeye değerdir. Güvenilirlik, rastgele değişken arıza zamanının (Tf) kümülatif dağılım fonksiyonunun (CDF) tamamlayıcısı iken, arıza oranı λ(t) koşullu olasılık yoğunluk fonksiyonudur ve şu şekilde tanımlanır:

$$\lambda \left( t \right) \equiv \frac{{\Pr \left( {\left. {t < T_{\mathrm {f}} \le t + {\mathrm {d}}t} \right|T_{\mathrm {f}} > t} \right)}}{{{\mathrm {d}}t}} = - \frac{1}{{S\left( t \right)}}\frac{{{\mathrm {d}}S\left( t \right)}}{{{\mathrm {d}}t}}$$

(2)

Başka bir deyişle, t zamanına kadar henüz gerçekleşmemiş olması şartıyla, t ile t + dt arasında bir arızanın gerçekleşme olasılığıdır.

Bunun Roma imparatorlarıyla ne ilgisi var? Coleridge'in arkadaşının aksine olmadıkları, şiddetli ölüm zamanlarını bir rastgele değişken olarak ele alabilir ve aynı güvenilirlik mühendisliği araçlarıyla veya daha geniş anlamda yaşam verisi analizi istatistiksel araçlarıyla inceleyebileceğimizdir - çift anlamlılık (yaşam) kasıtlı değildir ancak kaçınılmazdır burada.

Hayatta kalma analizi olarak da bilinen yaşam verisi analizi, olay zamanının bir rastgele değişken olarak analizini ve olasılıklı modellemesini ifade eder. Olay geniş bir şekilde tanımlanabilir ve çeşitli akademik disiplinler bu istatistiksel aracı kendi özel ilgi alanları için benimsemiştir. Örneğin, ilginin bir eşyanın arıza zamanında olduğu güvenilirlik mühendisliğinin ötesinde, hayatta kalma analizi ayrıca tıbbi araştırma ve halk sağlığında da yaygın olarak kullanılır; burada ilgi, örneğin bir hastalığın gelişme zamanı, tedaviden sonra remisyon zamanı veya prognotikten sonra ölüm zamanıdır. Bu olayları daha fazla nitelendirmek için daha fazla ayrıntı eklenebilir. Hayatta kalma analizi ayrıca, örneğin ateşkeslerin bozulma zamanını, mezuniyetten sonra ilk iş bulma zamanını veya bir kişinin ilk çocuğuna sahip olma zamanını incelemek için nicel siyasi bilim ve sosyolojide giderek daha fazla kullanılmaktadır.

Bir sonraki bölüm, bu istatistiksel araçların uygulama alanını beklenmedik bir nüfusa, Roma imparatorlarına genişletiyor ve güvenilirlik mühendisliğinin odağına benzer olmayan, ancak arıza zamanları yerine şiddetli ölüm zamanlarını inceliyor.

Bu çalışma için veriler, Roma imparatorlarının hakemli çevrimiçi bir ansiklopedisi olan De Imperatoribus Romanis'ten (DIR) elde edildi [DIR] (De Imperatoribus Romanis DIR, 2019). Her imparator için giriş, alandaki önde gelen bir bilim insanı tarafından yazılmıştır. İmparatorluk Dizini, birleşik Roma İmparatorluğu'nun hükümdarlarının listesini ve mantoyu başarısız bir şekilde talep eden birçok gaspçıyı sağlar. Veriler oldukça standart ve genel olarak kabul edilmekte olup, sonuç olarak daha fazla kalite kontrolüne tabi tutulması, bu çalışmanın kapsamının ötesinde kabul edildi. Burada yalnızca Roma senatosu tarafından onaylanan meşru imparatorlar dikkate alınmaktadır.3

Örneğin, hem Commodus'un4 (ö. 192 MS) hem de Pertinax'ın (ö. 193 MS) öldürülmesini izleyen sorunlu dönemden sonra, Roma tarihinde not edilmiş bir olay gerçekleşti: pretoryen muhafızları imparatorluğu fiilen en yüksek teklif verene, Didius Julianus'a sattı. Bu utanç verici olaya "imparatorluğun açık artırması" adı verildi ve pretoryenlerin imparator yapıcılar olarak hareket ettiği ilk veya son kez değildi (böyle bir olayın ilk örneği, Gaius Küçük Ayakkabı veya askerleri tarafından takma adıyla anılan Caligula'nın öldürülmesini takiben Claudius'un seçilmesiydi; ünlü babası Germanicus). Didius Julianus, halefi Septimius Severus ve diğerleri tarafından gaspçı olarak kabul edilmiş olsa da, senato tarafından ilan edilmiş olması onu bizim amaçlarımız için "meşru" bir imparator yapar. Yan not olarak, Didius Julianus, imparator olmanın biçimi ve idam edilmeden önce 66 gün süren en kısa saltanatlardan birine sahip olmasıyla dikkat çekicidir.

Bahsedilmesi gereken verilerle ilgili bir başka nokta da sansürdür. İstatistiksel anlamda sansür, bir dizi eşyanın analizine yönelik yaşam verilerinin "eksik" olması durumunda meydana gelir. Bu durum tıbbi araştırmalarda ve güvenilirlik mühendisliğinde sıklıkla meydana gelir ve çalışma altındaki bazı bireylerin takibe alınmaması veya bazı eşyaların arızanın veya ilgi konusu olayın gözlemlenmesinden önce çıkarılması nedeniyle olabilir. Bizim durumumuzda, bireylerin yaklaşık %38'i, hastalıktan veya yaşlılıktan öldükleri için (sağdan) sansürlenmiştir. Ancak Diocletianus ve Maximianus adlı iki imparator, başka bir olasılık dışı mekanizma aracılığıyla sansürlenmiştir: tahttan çekilme. Diocletianus, 284 MS'de imparator olmak için askeri rütbelerden yükseldi ve genç Alexander Severus'un (ö. 235 MS) öldürülmesinden bu yana üçüncü yüzyılın çoğunu etkileyen imparatorluk krizine son verdi. Diocletianus ayrıca, Roma İmparatorluğu'na en azından Doğu'da yüzyıllarca daha ömür veren birçok idari ve askeri reform yaptı. Daha sonra, 305 MS'de tahttan çekildi ve hayatının geri kalanını güzel Hırvat kıyısındaki Split'teki sarayında bahçıvanlığa adadı.5 (ö. 316 MS). Bu nedenle, bu çalışmanın amacı için, Diocletianus ve muhtemelen istemeyerek tahttan çekilen ortak imparatoru Maximianus, bu analize sansürlenmiş yaşam verileri katkıda bulunmaktadır. Maximianus'un tahttan çekildikten 5 yıl sonra öldürülmesi veya intihar etmesi, şiddetli bir ölümle karşılaşan imparatorlar arasında sayılması için yeterli değildir, çünkü artık imparator değildi.

Kaynakların kalitesi ve sınırlaması, bir imparatorun ölümü veya suikasti gibi büyük olaylar için bile kabul edilmelidir. Buradaki ilgi konusu olan antik tarihin kaynakları eşitsiz bir şekilde dağılmıştır. Bazen yamalı, bazen çelişkili ve sık sık ima ve çıkarımlarla ilerler. Örneğin, Suetonius, Caligula'nın veya bir hizmetkarın, ikincisi hastalandıktan sonra İmparator Tiberius'u (ö. 37 MS) zehirlemiş veya boğmuş olabileceğine dair birkaç söylenti anlatır. Bu imparatorun Roma'daki tüm sosyal sınıflarda uyandırdığı nefret derecesi, bu söylentilere katkıda bulunmuş olabilir. Ancak Tiberius'un ölümünün kötü niyetli bir eylem sonucu olma olasılığı düşüktür ve genel fikir birliği bu olasılıktan uzaklaşmaktadır. Bununla birlikte, antik tarihle ilgili şeylerde bu belirsizlik sorunu, özellikle rekabetçi anlatıların mevcut olduğu şüpheli imparator ölümleri durumunda ele alınmalıdır. Benzer bir durum Claudius'ta (ö. 54 MS) meydana gelir, ancak bu durumda genel fikir birliği, gerçekten de oğlu Nero'nun tahta çıkışını hızlandırmak için karısı Agrippina tarafından zehirlendiğidir. Bu çalışmanın amacı için, Claudius bu nedenle şiddetli bir ölümle karşılaşanlar arasında sayılırken, Tiberius sayılmaz.

İki durum daha, hem gariplikleri hem de Tiberius ve Claudius'un ölümleriyle sundukları paralellik nedeniyle dikkat çekicidir. Numerianus, 283 MS'de babasının ölümünden sonra Avgustus ilan edildi. Pretoryen muhafızlarının prefektörünün kızı Flavius Aper ile evliydi. Suriye'den dönerken genç imparator hastalandı ve Aper de dahil olmak üzere çevresi, imparatorun göz iltihabı olduğunu ve bu nedenle kapalı bir sedyede seyahat etmesi gerektiğini duyurdu. Birkaç gün boyunca, onu bekleyen askerler çürüme kokusunu fark edene kadar kimse imparatoru ziyaret etmedi. Sedyayı ancak imparatorun çürüyen cesedini bulduklarında açtılar. İmparatorluk komutanı Aper'i bu aşağılık fiilden suçladı ve onu öldürdü. Askerler daha sonra bu komutanı, Valerius Diocles'i imparator ilan etti ve o askeri ve idari olarak en yetenekli imparatorlardan biri olan Diocletianus olacaktı. Öyleyse bu hikayeden ne çıkarmalıyız? Numerianus gizemli koşullar altında ölüyor. Ama kayınpederinin yerini almak ve mantoyu üstlenmek için damadını ortadan kaldırmanın Aper'in isteği miydi? Diocles daha kurnazca aldatıcı mıydı ve hem imparatoru hem de Pretoryen Prefektörünü ortadan kaldırarak imparator oldu mu? Yoksa Numerianus sadece şanssız mıydı ve hastalığına yenik düştü, ardından olaylar rastgele geliştiler mi? Bu noktada sadece spekülasyon yapılabilir ve bu sorunlar çözülemez. Bu çalışmanın amacı için Numerianus'un ölümü, Tiberius'unkine benzer şekilde ele alınmaktadır, yani kötü niyetli bir eylem sonucu olarak kabul edilmemektedir. Benzer bir durum yaklaşık 40 yıl önce, çocuk imparator Gordian III'ün (ö. 244 MS) şüpheli ölümüyle meydana geldi. Yeni atanan Pretoryen Prefektörü Julius Philippus'un, daha sonra Arap Filipus imparatoru, bu olayda şüphelidir. Bunlar yine spekülasyondur ve bu çalışmanın amacı için Gordian III'ün ölümü Tiberius'unkine benzer şekilde ele alınmaktadır. Bu nedenle, aşağıdaki istatistiksel sonuçlar ihtiyata dayalıdır ve büyük olasılıkla muhafazakardır.

Bu verilerle ilgili can sıkıcı küçük sorunların yanı sıra, bu çalışmadaki istatistiksel analizlerin geri kalanı basittir: sansürlenmiş verileri işlemek için parametrik olmayan Kaplan-Meier tahmincisi ile başlar, ardından belirli bir olasılık dağılım fonksiyonunun parametrelerini tahmin etmek için en büyük olabilirlik yöntemine devam eder.6 Hükümdarlığının ilk yılında şiddetli bir ölümle karşılaşan imparatorlara 0.5 yıllık bir saltanat atanır, çünkü tam gün sayısı her zaman doğru bir şekilde bilinmemektedir. Hükümdarlığın ilk yılından sonra, süre ölümün gerçekleştiği yıla kadar yuvarlanır. Veriler ekte Tablo A1'de verilmiştir.

Bu bölümde, bir Roma imparatorunun şiddetli ölümünün görünüşte rastgele stokastik sürecinin zamansal imzasını inceliyoruz. Ayrıca, bu sürecin rastgeleliğinin altında bazı yapıların olup olmadığını inceliyoruz ve güvenilirlik mühendisliğindeki sonuçlarla paralellikleri tartışıyoruz.

Parametrik olmayan ve parametrik analizler ve yorumlama

Tablo A1'deki veriler Kaplan-Meier tahmincisi ile işlenir ve sonuçlar Şekil 2'de verilmiştir. En uzun saltanat, erken imparatorluğun adlandırıldığı şekilde prensipatı kuran Avgustus'a aitti. 45 yıl hüküm sürdü ve huzur içinde yaşlılıktan öldüğü için analize sansürlenmiş veriler katkıda bulunur. Şekil 2'deki sonuçlar bu son şiddetli ölüm zamanına kadar gösterilmektedir.

Şekil 2 şu şekilde okunur: Örneğin 3 yıllık noktada, bir imparatorun şiddetli bir ölümle karşılaşmamış olma şansı %64'tü; 7 yıllık noktada bu şanslar %50'ye, yani sıradan bir yazı tura atmaya düşüyor. Şiddetli ölüm olasılığı bu rakamların tamamlayıcısıdır, sırasıyla %36 ve %50.

Bu ne anlama geliyor? Bu şekilde önemli üç belirgin özellik dikkat edilmelidir:

ben.

İmparatorlar, hükümdarlıklarının ilk yılında şiddetli ölüm riskiyle önemli ölçüde karşı karşıya kaldılar. Bu risk yüksek kaldı ancak sonraki 7 yıl boyunca giderek azaldı. Bu, güvenilirlik mühendisliğinde bebek ölüm oranını anımsatır; zayıf bileşenlerin hizmete girdikten kısa bir süre sonra, örneğin tasarım veya üretim kusurları nedeniyle erken başarısız olduğu bir evre. Bu nedenle, Roma imparatorları bir tür bebek ölüm oranı yaşadılar;

ii.

Güvenilirlik veya hayatta kalma fonksiyonu 8. yıl hükümdarlıktan sonra stabilize olur. İmparatorlar, 8 yıla ulaşırlarsa biraz daha rahatlayabilirlerdi...

iii.

...ama uzun sürmez: şiddetli ölüm riski, 12 yıllık hükümdarlıktan sonra tekrar artar. Bu, yeni mekanizmaların veya süreçlerin bir başka cinayet turuna yol açtığını göstermektedir. Bu, güvenilirlik mühendisliğinde yıpranma süresini anımsatır; bileşenlerin, özellikle mekanik eşyaların, yorgunluk, korozyon veya yıpranma nedeniyle arıza oranının arttığı bir evre. Bu nedenle, Roma imparatorları da yıpranma ölüm oranı yaşadılar.

Önceki parametrik olmayan sonuçlar için bir Weibull grafiği Şekil 3'te verilmiştir. Grafik, ln(t) fonksiyonu olarak ln{−ln[S(t)]}'yi gösterir. Elde edilen veri noktaları hizalıysa, verilerin etkili bir şekilde bir Weibull dağılımından kaynaklandığı sonucuna varılabilir, yani bu şiddetli ölüm sürecine yol açan altta yatan parametrik dağılım gerçekten bir Weibull'dür. Weibull hayatta kalma fonksiyonu, güvenilirlik mühendisliğinde ve hayatta kalma analizinde yaygın olarak kullanılır çünkü oldukça esnek bir parametrik modeldir ve şu şekilde verilir:

$$S\left( t \right) = {\mathrm {exp}}\left[ { - \left( {\frac{t}{\theta }} \right)^\beta } \right]$$

(3)

β şekil parametresi ve θ (zamansal) ölçek parametresi veya karakteristik yaşam olarak adlandırılır. 1'den küçük bir şekil parametresi β, çalışma altındaki eşyalarda bebek ölüm oranının yaygınlığını gösterir veya yansıtırken, β > 1, yıpranma arızalarının yaygınlığını gösterir (sırasıyla azalan ve artan arıza oranları). Denklem (3), doğrusal bir Weibull grafiğine (Denklem (4)) eşdeğerdir:

$${S}\left( {t} \right) = {{\mathrm {exp}}}\left[ { - \left( {\frac{{t}}{\theta }} \right)^\beta } \right] \Leftrightarrow \ln \left\{ { - \ln \left[ {{S}\left( {t} \right)} \right]} \right\} = \beta \ln \left( {t} \right) - \beta \ln \left( \theta \right)$$

(4)

Uzun bir dört yüzyıllık dönem boyunca ve çok değişen bir dünyada, bir Roma imparatorunun şiddetli ölümü gibi alışılmadık ve rastgele bir stokastik sürecin sistematik bir altta yatan yapısının olması ve bir Weibull dağılımı tarafından dikkate değer bir şekilde yakalanması ilginçtir. Bu sonucun tamamen gereksiz olması, ürkütücülüğünü azaltmaz!

Bu altta yatan yapı neden? İstatistiksel teoride, Weibull fonksiyonu, çok sayıda rastgele gözlemin minimum değerini yakalayan bir ekstrem değer dağılımıdır. Bu noktayı açıklığa kavuşturmak için, örneğin belirli bir işlevi yerine getirmek için seri olarak yerleştirilmiş çok sayıda n bileşene sahip bir sistemi ele alalım. Herhangi bir bileşenin arızası, sistemin arızasıyla sonuçlanır, işlevi artık sağlanmaz. Bu nedenle, sistemin arıza zamanı, herhangi bir bileşeninin arıza zamanının minimum zamanıdır. İstatistiksel ekstrem değer teorisi, bileşenlerin altta yatan arıza dağılımından bağımsız olarak, n çok büyük olduğunda, sistemin arıza zamanının bir Weibull dağılımına yaklaştığını bize söyler. Bu örnekte, bileşen düzeyi ve sistem düzeyi hususları arasındaki farkı ve toplu sistem düzeyindeki sonucun herhangi bir bileşenin arıza dağılımından bağımsız olmasını fark edin. Ekstrem değer teorisi, ilgili başka bir bağlamda da geçerlidir: Tek bir monolitik eşyayı ele alalım. Bu eşyada bileşen yok. Ancak, bu eşyanın n farklı rekabetçi arıza süreci olduğunu varsayalım, hangisi önce olursa olsun eşyayı bozar. n çok büyük olduğunda, bu da her arıza sürecinin dağılımından bağımsız olarak eşyanın arıza zamanında bir Weibull dağılımıyla sonuçlanacaktır.

Bu gözlemlerin Roma imparatorlarının şiddetli ölümüne genişletilmesi ihtiyatla yapılmalıdır. Ancak yine de keşif için verimli bir alan sunmaktadır. Burada ilgi konusu olan stokastik sürecin zaman imzasının bir Weibull dağılımı tarafından dikkate değer bir şekilde yakalanmış olması, bunun belki de imparatoru şiddetli bir şekilde ortadan kaldırmak için komplo kuran çok sayıda altta yatan sürecin sonucu olduğunu düşündürmektedir. İmparatorun şiddetli ölümüne birçok yolun olması, korkunç görevi üstlenmek için çok sayıda bireyin ve motivasyonun olması, Weibull'u, bir ekstrem değer dağılımını, bu durumda teorik olarak olası kılmaktadır.

Karışım Weibull dağılımları

Şekil 3'ün daha yakından incelenmesi, Şekil 2'de görülen yıpranma arızalarının başlangıcına karşılık gelen ln(t) ≈ 2.5'ten önce ve sonra veri noktaları için iki farklı eğim göstermektedir. Bu nedenle, verilere bir karışım Weibull dağılımı uygulanır ve parametrelerinin en büyük olabilirlik tahminleri şu şekilde verilmiştir:

$$\begin{array}{l}\widehat S\left( t \right) = 0.876 \cdot {\mathrm {exp}}\left[ { - \left( {\frac{t}{{12.835}}} \right)^{0.618}} \right] + 0.124 \cdot {\mathrm {exp}} \left[ { - \left( {\frac{t}{{14.833}}} \right)^{13.387}} \right]\end{array}$$

(5)

Denklem (5), önceki gözlemlerin analitik bir doğrulamasını sağlar; Roma imparatorları şiddetli ölüm şeklinde hem bebek ölüm oranı (β = 0.618) hem de yıpranma ölüm oranı (β = 13.387) yaşadılar. Bu parametrik sonuç Şekil 4'te gösterilmektedir.

Bebek ölüm oranı yaşayan imparatorlar, kullanıma girdikten sonra erken arızalar yaşayan mühendislik bileşenlerinden farklı değildi: tasarım açısından zayıf veya çevrelerinin ve koşullarının taleplerini karşılamada temelde yetersiz. Her yüzyıldan örnekler mevcuttur, örneğin Galba (ö. 69 MS), Pertinax (ö. 193 MS), Macrinus (ö. 218 MS) ve Severus II (ö. 307 MS). Bunlar kargaşa zamanlarıydı ve ilk iki durumda, bunlar yeni hanedanlara (sırasıyla Flavian ve Severan) geçiş zamanlarıydı. İmparatorların bebek ölüm oranı, kısmen hem kriz ve istikrarsızlık zamanlarının nedenleri hem de sonuçları olarak görülebilir.7

Yıpranma ölüm oranı yaşayan imparatorlar, farklı arıza mekanizmalarıyla sonlarını buldular. Öncelikle bazı mühendislik bileşenlerinin uzun süre hizmet verdikten sonra arızalarda bir artış (yıpranma arızaları) yaşadıklarını göz önünde bulundurun. Başlangıçta sağlam olabilirler ve başlangıçta ılımlı çalışma ortamlarından faydalanmış olabilirler. Ancak bozulma, yorgunluk veya çalışma ortamında artan sertlik yoluyla, yıpranma arızaları yaşamaya başlarlar. Şekil 2'de görüldüğü gibi, hükümdarlıklarının ilk 8 yılını atlatan imparatorların yaklaşık 4 yıllık bir müsamaha süresi vardı. Şiddetli ölüm daha sonra onlara geldi (yıpranma ölüm oranı), çünkü örneğin eski düşmanları yeniden gruplanmış veya yenileri ortaya çıkmıştı, çünkü giderek artan sayıda tarafı yabancılaştırmışlardı veya imparatorluk yönetiminde yeni zayıflıklar ortaya çıkmış veya büyümüştü. Şekil 3'te ve Denklem (5)'teki her Weibull dağılımının farklı karakteristik yaşam parametrelerinde görüldüğü gibi, bu yeni öldürücü süreçlerin, imparatorların bebek ölüm oranını yönlendiren süreçlerden farklı bir zamansal imzası olduğu açıktır. Örneğin, 15 yıllık bir hükümdarlıktan sonra Domitian'ın ölümü (ö. 96 MS) veya 12 yıllık bir hükümdarlıktan sonra Commodus'un ölümü (ö. 192 MS) veya 15 yıllık bir hükümdarlıktan sonra Gallienus'un ölümü (ö. 268 MS), yıpranma ölüm oranını göstermektedir.8

Parametrik uydurmanın (Denklem (4)) arıza oranı (Denklem (2)) Şekil 5'te verilmiştir. Sonuç, çok sayıda mekanik ve elektronik bileşen için yaygın olarak kullanılan ve ampirik olarak doğrulanan dikkate değer bir küvet benzeri eğri göstermektedir. Bu nedenle, Roma imparatorları, bu mühendislik eşyaları gibi, küvet benzeri bir arıza oranı yaşadılar.

Şekil 5'teki sonuçlar ilginç bir yorum sunmaktadır:

ben.

Başlangıçta azalan arıza oranı, bebek ölüm oranının imzası, daha önce belirtildiği gibi, başlangıçta çevrelerinin ve koşullarının taleplerini ele alamayan zayıf imparatorların yaygınlığını yansıtır. Bununla birlikte, arıza oranının azalması, bir yandan imparatorları şiddetli bir şekilde ortadan kaldırmaya çalışan (ortadan kaldırma) ve diğer yandan imparatorların kendilerini daha iyi korumayı ve belki de rakiplerini ortadan kaldırmayı öğrenme eğrisini yansıtan (koruma) süreçler arasında bir rekabeti göstermektedir. Roma tarihinde bu rekabetin örnekleri mevcuttur. Birinin hükümdarlığının ilk 12 yılına kadar, koruma süreçleri performanslarını istikrarlı bir şekilde iyileştirdi ve durum rahatlıkla "onları [Roma imparatorlarını] öldürmeyen her şey onları güçlendirdi" veya şiddetli bir ölümle karşılaşma olasılıklarını azalttı şeklinde özetlenebilir;

ii.

12 yıllık hükümdarlıktan sonra artan arıza oranı, yıpranma arızalarının imzası, daha önce belirtildiği gibi, zamanla bozulma, yorgunluk veya koşullarında artan sertlik yoluyla arızalarda bir artışı yansıtır. Değişen (jeo-)politik koşullar altında yetenekler ve talepler arasında artan bir uyumsuzluk. Bu, daha önce tartışılan bir dizi nedenden kaynaklanabilir. Bu 12 yıllık noktadan sonra arıza oranının artması, (i)'de belirtilen aynı karşıt süreçler arasında bir rekabeti tekrar göstermektedir ve bu sefer koruma süreçleri bu rekabetin kaybettiği tarafındaydı. Bu sonuç, 12 yıllık bir hükümdarlıktan sonra "onları öldürmeyen her şey onları zayıflattı" şeklinde nedensel olarak özetlenebilir.

Bu özel ayrıntıların ötesinde, burada incelenen tarihi bir stokastik süreç içinde tutarlı bir yapı bulmanın ne anlama geldiğini söyleyelim? Kabaca konuşursak, sonuç, burada incelenen olgunun altta yatan rastgeleliğinin üzerine bindirilmiş, ortalama bir anlamda veya beklenen değer olarak sistemik faktörlerin ve belirli bir determinizm seviyesinin varlığını ima eder. Başka bir deyişle, süreç tamamen rastgele değildir; rastgeleliğinin üzerine bindirilmiş bazı deterministik faktörleri vardır. Conan Doyle, Sherlock Holmes: The Sign of Four'de, bu genel fikri oldukça doğru bir şekilde şu şekilde ifade etmiştir:

Bireysel insan çözülemeyen bir bilmeceyken, toplu halde matematiksel bir kesinlik haline gelir. Örneğin, herhangi bir insanın ne yapacağını asla tahmin edemezsiniz, ancak ortalama bir sayının ne yapacağını kesinlikle söyleyebilirsiniz.

Bu bölümdeki sonuçlar, Roma imparatorlarının şiddetli ölümünün altında benzer bir fikrin yattığını düşündürmektedir.

Etiyoloji ve gelecek çalışmalar için öneri

Önceki alt bölümler, burada incelenen olgunun, imparatorların şiddetli ölümü, gladyatör oyunlarına benzemeyen bir vahşet ve şiddet gösterisinin zamansal imzasını inceledi, ancak dört yüzyıla yayıldı ve tüm Roma dünyasını etkiledi (Millar, 1977).

İncelenmeyen şey, bu olgunun etiyolojisi veya nedensel temeli veya imparatorların neden sürekli olarak şiddetli ölümlerle karşılaştıklarıdır, yalnızca zaman içinde değil, nasıl. Roma imparatorlarının şiddetli ölümlerinin doğrudan nedenleri literatürde sıklıkla tartışılmaktadır. Örneğin Scarre'nin (1995) "Roma İmparatorlarının Kronolojisi"'nde bulunabilir ve Retief ve Cilliers'in (2005) "Sezarlar Arasındaki Ölüm Nedenleri (MÖ 27-MS 476)" adlı eserinde kısa bir özet verilmiştir. Girişler, "kılıç/hançerle öldürüldü [...]", "[bireyin adı] tarafından zehirlendi" veya "askerler tarafından başı kesildi" gibi ifadeler içerir. Bu açıklamaların önemi azdır ve bu bağlamda nedenselliğin karmaşık yapısını yansıtmamaktadır. Burada incelenen olgunun nedensel temeli, Roma tarihi, Roma monarşisinin gelişimi ve patolojileri, imparatorluk mirasının problemi, pretoryen muhafızının rolü, lejyonların sadakati ve imparatorluğun coğrafi genişliği ve kaynakları gibi bir dizi temel konuyu kesişmektedir. Bu konular ve burada incelenen olguyla ilişkilerinin karmaşık doğası